Streaming Convolutions
Motivation
A common model architecture in speech processing takes a waveform as input or output a waveform. Some examples include Encodec or HiFi-GAN. However, real-world deployments of these architectures usually need to process a stream of input waveform batches, which can cause issues when the convolutional architecture has overlapping receptive fields. This is relatively easy to work around, but a cursory search didn't yield a straightforward reference for the math involved, so I'm going to write one up here.
Convolution
First we'll consider the receptive fields for a vanilla convolution with various parameters.
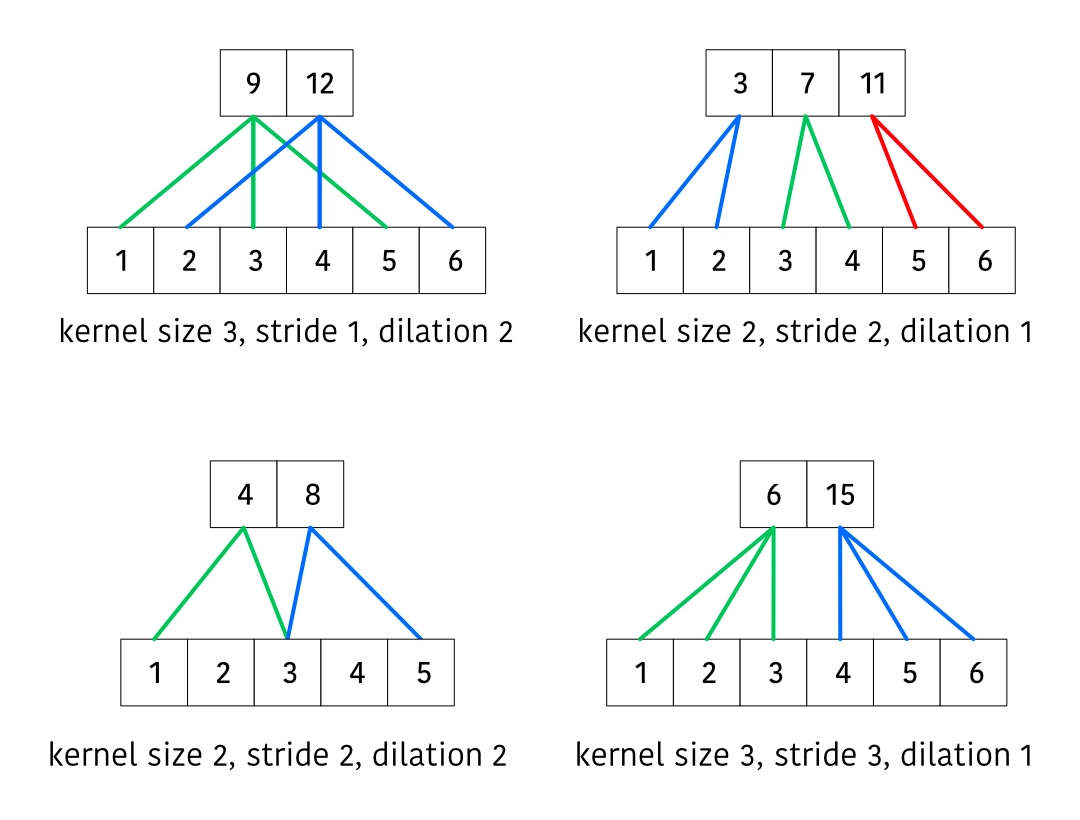
The second output takes the input shifted by , the third output takes the input shifted by , and so on. This means that after computing our convolution, we can discard the first samples in our state, where is the number of output samples.
A slight nuance is when the input contains fewer than samples. In this case, we need to keep track of the leftover amount that we need to discard, so that on the next batch we can discard whatever remaining inputs.
I've implemented a function for doing this in PyTorch below.
View Code
def streaming_conv_1d(
x: Tensor,
state: tuple[Tensor, int] | None,
weight: Tensor,
bias: Tensor | None,
stride: int,
dilation: int,
groups: int,
) -> tuple[Tensor, tuple[Tensor, int]]:
"""Applies a streaming convolution.
Args:
x: The input to the convolution.
state: The state of the convolution, which is the part of the previous
input which is left over for computing the current convolution,
along with an integer tracker for the number of samples to clip
from the current input.
weight: The convolution weights.
bias: The convolution bias.
stride: The convolution stride.
dilation: The convolution dilation.
groups: The convolution groups.
Returns:
The output of the convolution, plus the new state tracker.
"""
pre_x = state[0] if state is not None else None
pre_t = state[1] if state is not None else 0
if pre_x is not None:
x = torch.cat((pre_x, x), dim=-1)
if pre_t > 0:
pre_t, x = pre_t - x.shape[-1], x[..., pre_t:]
(bsz, _, tsz), (chsz_out, _, ksize) = x.shape, weight.shape
min_tsz = 1 + (ksize - 1) * dilation
if tsz < min_tsz:
return x.new_zeros(bsz, chsz_out, 0), (x, pre_t)
y = F.conv1d(x, weight, bias, stride, 0, dilation, groups)
t = stride * y.shape[-1]
return y, (x[:, :, t:], max(0, t - tsz))
I've implemented this module and unit test in my ML boilerplate library here.
Transposed Convolution
Next we'll consider a transposed convolution.
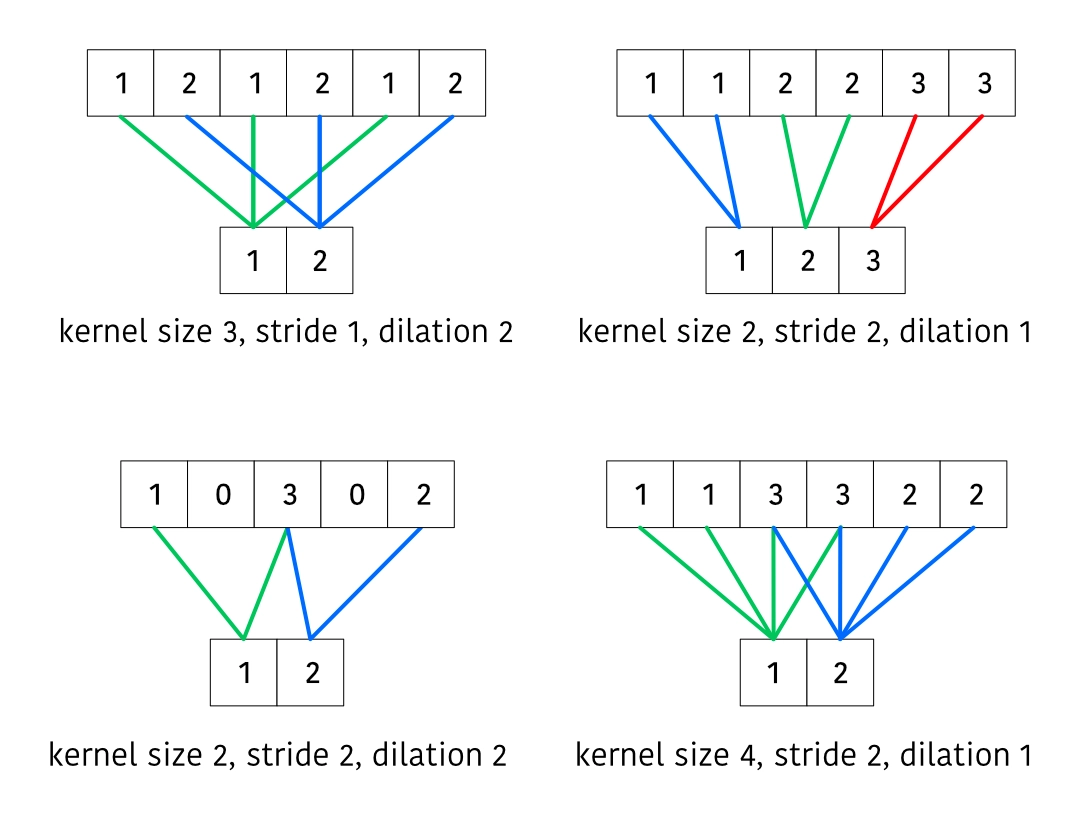
Note that we have to slightly shift our thinking for transposed convolutions. We can consider the first output samples to be "done" (meaning, additional inputs won't change any of their values). We can cache the other outputs and add them to the outputs on the next step.
There's a few additional nuances here:
- We need to avoid duplicating biases when adding together outputs on subsequent steps
- Similarly to earlier, if the number of output samples is less than , we need to keep track of the leftover amount and prepend zeros to the next set of outputs
I've implemented a function for doing this in PyTorch below.
View Code
def streaming_conv_transpose_1d(
x: Tensor,
state: tuple[Tensor, int] | None,
weight: Tensor,
bias: Tensor | None,
stride: int,
dilation: int,
groups: int,
) -> tuple[Tensor, tuple[Tensor, int]]:
"""Applies a streaming transposed convolution.
Args:
x: The input to the convolution.
state: The state of the convolution, which is the part of the previous
input which is left over for computing the current convolution,
along with an integer tracker for the number of samples to clip
from the current input.
weight: The convolution weights.
bias: The convolution bias.
stride: The convolution stride.
dilation: The convolution dilation.
groups: The convolution groups.
Returns:
The output of the convolution, plus the new state tracker.
"""
y = F.conv_transpose1d(x, weight, bias, stride, 0, 0, groups, dilation)
post_y = state[0] if state is not None else None
post_t = state[1] if state is not None else 0
bsz, chsz_out, tsz = y.shape
if post_t > 0:
init_y = y.new_zeros(bsz, chsz_out, post_t)
if bias is not None:
init_y += bias[..., None]
y = torch.cat([init_y, y], dim=-1)
if post_y is not None:
n = min(post_y.shape[-1], y.shape[-1])
init_y = post_y[..., :n] + y[..., :n]
if bias is not None:
init_y -= bias[..., None]
y = torch.cat((init_y, post_y[..., n:], y[..., n:]), dim=-1)
t = stride * x.shape[-1]
return y[..., :t], (y[..., t:], max(0, t - tsz))