Fast Attention Implementations

I realized recently that there's a ton of papers out there that purport to deliver faster self-attention implementations. In this post I'll list some of the approaches which I'm familiar with and provide some PyTorch code snippets explaining the key ideas behind each of them.

This collection is heavily cut down from the very wide variety of papers purporting to implement improvements to attention. I've tried to focus on the ones that I think are important, although there are likely many that I've missed. If you think I've missed something important, please let me know!

Linformer

Time complexity: $O(t)$ , space complexity: $O(t)$

import torch
import torch.nn.functional as F
from torch import Tensor, nn

class LinformerAttention(nn.Module):
    def __init__(self, dim: int, seq_len: int, heads: int, k: int) -> None:
        super().__init__()

        assert dim % heads == 0

        # Stores constant values.
        self.seq_len = seq_len
        self.k = k
        self.heads = heads
        self.dim_head = dim // heads

        # Similar to the original transformer implementation, but with two
        # extra parameters for projecting from the full sequence length.
        self.to_q = nn.Linear(dim, dim, bias=False)
        self.to_k = nn.Linear(dim, dim, bias=False)
        self.to_v = nn.Linear(dim, dim, bias=False)
        self.proj_k = nn.Parameter(torch.empty(seq_len, k))
        self.proj_v = nn.Parameter(torch.empty(seq_len, k))
        self.to_out = nn.Linear(dim, dim)

    def forward(self, x: Tensor) -> Tensor:
        (b, n, d), d_h, h, k = x.shape, self.dim_head, self.heads, self.k

        # Applies the input projection layers.
        queries = self.to_q(x)
        keys = self.to_k(x)
        values = self.to_v(x)

        # Projects from the low-rank dimension to the full sequence length.
        keys = torch.einsum("bnd,nk->bkd", keys, self.proj_k)
        values = torch.einsum("bnd,nk->bkd", values, self.proj_v)

        # Reshapes the queries, keys, and values for the attention operation.
        queries = queries.reshape(b, n, h, -1).transpose(1, 2)  # (B, N, D) -> (B, H, N, D // H)
        keys = keys.reshape(b, k, h, -1).transpose(1, 2)  # (B, K, D) -> (B, H, K, D // H)
        values = values.reshape(b, k, h, -1).transpose(1, 2)  # (B, K, D) -> (B, H, K, D // H)

        # Vanilla dot-product attention.
        out = F.scaled_dot_product_attention(queries, keys, values)

        # Reshapes to the expected output shape.
        out = out.transpose(1, 2).reshape(b, n, -1)  # (B, H, N, D // H) -> (B, N, D)

        return self.to_out(out)

if __name__ == "__main__": # Small test script.
    attn = LinformerAttention(dim=16, seq_len=32, heads=4, k=2)
    x = torch.randn(1, 32, 16)
    y = attn(x)
    assert x.shape == y.shape

Low-rank factorization of the full attention. The main idea is that self-attention is low-rank, especially for higher layers (i.e., sparse, only attending to a small number of values). So you can just approximate the full attention matrix using SVD.

Figure 2 from the Linformer paper, demonstrating how to factorize the $K$ matrix, where $n$ is the number of time steps, $k$ is the low-rank dimension, and $d$ is the embedding dimension.

Performer

Time complexity: $O(t)$ , space complexity: $O(t)$

import torch
from torch import Tensor, nn


def causal_linear_attention(
    q: Tensor,
    k: Tensor,
    v: Tensor,
    chunk_size: int = 128,
    eps: float = 1e-6,
) -> Tensor:
    """PyTorch implementation of causal linear attention from Performer.

    This implementation is only partially complete.

    Args:
        q: The query tensor, with shape (batch_size, num_heads, seq_len, dim_head).
        k: The key tensor, with the same shape as the query tensor.
        v: The value tensor, with the same sahpe as the query tensor.
        chunk_size: The chunk size to use for the linear attention.
        eps: A small value to add to the denominator for numerical stability.

    Returns:
        The output of the causal linear attention, with the same shape as the
        input query, key and value.
    """

    last_k_cumsum: Tensor | None = None
    last_ctx_cumsum: Tensor | None = None
    outs = []

    for q, k, v in zip(*map(lambda t: t.chunk(chunk_size, dim=-2), (q, k, v))):
        k_cumsum = k.cumsum(dim=-2) if last_k_cumsum is None else last_k_cumsum + k.cumsum(dim=-2)

        d_inv = 1.0 / torch.einsum("bhnd,bhnd->bhn", q, k_cumsum.type_as(q) + eps)
        ctx = torch.einsum("bhnd,bhne->bhnde", k, v)
        ctx_cumsum = ctx.cumsum(dim=-3) if last_ctx_cumsum is None else last_ctx_cumsum + ctx.cumsum(dim=-3)
        out = torch.einsum("bhnde,bhnd,bhn->bhne", ctx_cumsum, q, d_inv)

        last_k_cumsum = k_cumsum[:, :, -1:]
        last_ctx_cumsum = ctx_cumsum[:, :, -1:]
        outs.append(out)

    return torch.cat(outs, dim=-2)


def get_qkv(x: Tensor, proj_dims: int | None) -> tuple[Tensor, Tensor, Tensor]:
    q, k, v = x, x, x
    if proj_dims is not None:
        proj = nn.init.orthogonal_(torch.empty(x.shape[-1], proj_dims))
        q, k = q @ proj, k @ proj
    q, k, v = q.softmax(-1), torch.exp(k), v
    return q, k, v


if __name__ == "__main__":
    x = torch.randn(1, 32, 16).unflatten(-1, (4, 4)).transpose(1, 2)
    q, k, v = get_qkv(x, 4)
    y = causal_linear_attention(q, k, v)
    assert x.shape == y.shape

Illustration of the Performer attention mechanism - by performing the $K^TV$ matrix multiplication first, using a low-rank value $r$ , we can avoid computing the full $A=QK^T$ and $AV$ outputs. The low-rank vectors $Q'$ and $K'$ are computed by applying a random feature map $\phi(u)$ to the original values, which can be shown statistically to well-approximate the original input space.

Also does a low-rank approximation of the full self-attention, by first projecting to a low-rank feature space using random orthogonal matrices.

Linear Transformer

Time complexity: $O(t)$ , space complexity: $O(t \log t)$

Similar to Performer, this paper uses kernel feature maps to express the attention mechanism as an RNN.

Attention-Free Transformer

There are several variants, with AFT-simple having $O(t)$ time and space complexity, AFT-full having $O(t^2)$ time complexity (but linear space complexity), and AFT-local (a.k.a. AFT-conv) having $O(ts)$ time complexity, where $s$ is some small window size.

Published in 2021
Apple blog
Arxiv

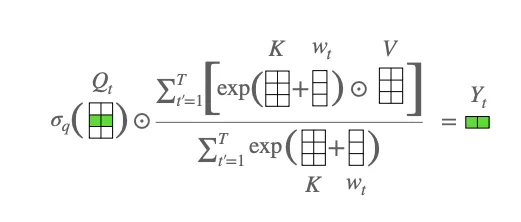
The attention-free transformer mechanism, from Figure 2 in the paper. $w$ is a positional embedding.

RWKV

def get_mask(tsz: int, device: torch.device | None = None, dtype: torch.dtype | None = None) -> Tensor:
    """Returns the forward mask, used for training.

    Args:
        tsz: The number of timesteps in the mask
        device: The mask device
        dtype: The mask dtype

    Returns:
        The forward mask, with shape (T, T)
    """
    mask = torch.empty(tsz, tsz, device=device, dtype=dtype)
    mask.fill_(float("-inf"))
    # mask.triu_(1)
    mask.tril_(-1)
    return mask


def run_wkv(
    tsz: int,
    w: Tensor,
    u: Tensor,
    k: Tensor,
    v: Tensor,
    last_num: Tensor,
    last_den: Tensor,
    mask: Tensor | None = None,
) -> tuple[Tensor, Tensor, Tensor]:
    """Runs the core WKV computation.

    Args;
        tsz: The number of timesteps
        w: The decay tensor, with shape (D)
        u: The output multiplier tensor, with shape (D)
        k: The K tensor, with shape (B, T, D)
        v: The V tensor, with shape (B, T, D)
        last_num: The last numerator, with shape (B, 1, D)
        last_den: The last denominator, with shape (B, 1, D)
        mask: The attention mask, with shape (T, T)

    Returns:
        The WKV tensor, with shape (B, T, D), and the next numerator and
        denominator tensors, each with shape (B, T, D)
    """
    assert w.dim() == u.dim() == 1
    assert mask is None or mask.dim() == 2
    assert k.dim() == v.dim() == last_num.dim() == last_den.dim() == 3

    t = torch.arange(tsz + 1, device=w.device)[None, :, None]
    wt = t[:, None, :-1, :] - t[:, :-1, None, :]
    w = -torch.exp(w)
    tw = w * t[:, 1:]
    twt = w * wt
    ktw = twt + k[:, :, None]
    if mask is not None:
        ktw = ktw + mask[None, :tsz, :tsz, None]

    etw, ektw = torch.exp(tw), torch.exp(ktw)
    num = etw * last_num + (ektw * v[:, :, None]).sum(1)
    den = etw * last_den + ektw.sum(1)

    last_num = torch.cat((last_num, num[..., :-1, :]), dim=-2)
    last_den = torch.cat((last_den, den[..., :-1, :]), dim=-2)

    out = (last_num + torch.exp(u + k) * v) / (last_den + torch.exp(u + k))

    return out, num, den


class Attention(nn.Module):
    init_x: Tensor
    init_num: Tensor
    init_den: Tensor
    mask: Tensor

    def __init__(self, emb_dim: int, max_tsz: int = 1024) -> None:
        super().__init__()

        self.time_decay = nn.Parameter(torch.empty(emb_dim))
        self.time_first = nn.Parameter(torch.empty(emb_dim))

        self.time_mix_k = nn.Parameter(torch.empty(1, 1, emb_dim))
        self.time_mix_v = nn.Parameter(torch.empty(1, 1, emb_dim))
        self.time_mix_r = nn.Parameter(torch.empty(1, 1, emb_dim))

        self.key = nn.Linear(emb_dim, emb_dim, bias=False)
        self.value = nn.Linear(emb_dim, emb_dim, bias=False)
        self.receptance = nn.Linear(emb_dim, emb_dim, bias=False)
        self.output = nn.Linear(emb_dim, emb_dim, bias=False)

        self.register_buffer("init_x", torch.zeros(1, 1, emb_dim), persistent=False)
        self.register_buffer("init_num", torch.zeros(1, 1, emb_dim), persistent=False)
        self.register_buffer("init_den", torch.zeros(1, 1, emb_dim), persistent=False)
        self.register_buffer("mask", get_mask(max_tsz), persistent=False)

    def time_shift(self, last_x: Tensor, x: Tensor) -> Tensor:
        _, tsz, _ = x.shape
        if tsz > 1:
            last_x = torch.cat((last_x, x[..., :-1, :]), dim=-2)
        return last_x

    def forward(self, x: Tensor, state: AttentionState) -> tuple[Tensor, AttentionState]:
        _, tsz, _ = x.shape

        last_x, last_num, last_den = (self.init_x, self.init_num, self.init_den) if state is None else state
        last_x = self.time_shift(last_x, x)

        k = self.key(x * self.time_mix_k + last_x * (1 - self.time_mix_k))
        v = self.value(x * self.time_mix_v + last_x * (1 - self.time_mix_v))
        r = self.receptance(x * self.time_mix_r + last_x * (1 - self.time_mix_r))
        sr = torch.sigmoid(r)

        w, u = self.time_decay, self.time_first
        wkv, num, den = run_wkv(tsz, w, u, k, v, last_num, last_den, self.mask)
        rwkv = wkv * sr

        return self.output(rwkv), (x[..., -1:, :], num[..., -1:, :], den[..., -1:, :])


class FeedForward(nn.Module):
    init_state: Tensor

    def __init__(self, emb_dim: int, ffn_dim: int) -> None:
        super().__init__()

        self.time_mix_k = nn.Parameter(torch.empty(1, 1, emb_dim))
        self.time_mix_r = nn.Parameter(torch.empty(1, 1, emb_dim))

        self.key = nn.Linear(emb_dim, ffn_dim, bias=False)
        self.receptance = nn.Linear(emb_dim, emb_dim, bias=False)
        self.value = nn.Linear(ffn_dim, emb_dim, bias=False)

        self.register_buffer("init_state", torch.zeros(1, 1, emb_dim), persistent=False)

    def time_shift(self, last_x: Tensor, x: Tensor) -> Tensor:
        _, tsz, _ = x.shape
        if tsz > 1:
            last_x = torch.cat((last_x, x[..., :-1, :]), dim=-2)
        return last_x

    def forward(self, x: Tensor, state: FeedForwardState | None = None) -> tuple[Tensor, FeedForwardState]:
        last_x = self.time_shift(self.init_state if state is None else state, x)

        k = self.key(x * self.time_mix_k + last_x * (1 - self.time_mix_k))
        r = self.receptance(x * self.time_mix_r + last_x * (1 - self.time_mix_r))
        vk = self.value(F.relu(k) ** 2)

        return torch.sigmoid(r) * vk, x[..., -1:, :]


class Block(nn.Module):
    def __init__(self, emb_dim: int, pre_norm: bool) -> None:
        super().__init__()

        self.ln0 = nn.LayerNorm(emb_dim) if pre_norm else None
        self.ln1 = nn.LayerNorm(emb_dim)
        self.ln2 = nn.LayerNorm(emb_dim)

        self.att = Attention(emb_dim)
        self.ffn = FeedForward(emb_dim, emb_dim * 4)

    def forward(self, x: Tensor, state: State | None = None) -> tuple[Tensor, State]:
        if self.ln0 is not None:
            x = self.ln0(x)
        dx, att_state_out = self.att(self.ln1(x), None if state is None else state[0])
        x = x + dx
        dx, ffn_state_out = self.ffn(self.ln2(x), None if state is None else state[1])
        x = x + dx
        return x, (att_state_out, ffn_state_out)


class Rwkv(nn.Module):
    def __init__(self, emb_dim: int, num_tokens: int, num_layers: int) -> None:
        super().__init__()

        self.emb = nn.Embedding(num_tokens, emb_dim)
        self.blocks = nn.ModuleList([Block(emb_dim, i == 0) for i in range(num_layers)])
        self.ln_out = nn.LayerNorm(emb_dim)
        self.head = nn.Linear(emb_dim, num_tokens, bias=False)

    def forward(self, tokens: Tensor, states_in: list[State] | None = None) -> tuple[Tensor, list[State]]:
        x = self.emb(tokens)
        states_out: list[State] = []
        for i, block in enumerate(self.blocks):
            x, state_out = block(x, None if states_in is None else states_in[i])
            states_out.append(state_out)
        x = self.head(self.ln_out(x))
        e_x = torch.exp(x - torch.max(x))
        probs = e_x / e_x.sum()
        return probs, states_out

A parallizable RNN, which can be trained like a transformer but can do infinite rollout (i.e., the memory buffer size does not grow with the number of decoded tokens). There's been a lot of inference implementations for this model.

This is an extension of the Attention-Free Transformer idea as a recurrent network. The recurrence relationship is defined as follows:

\begin{aligned} \alpha_i & = \sum_{j=1}^i e^{-(i-j)w+k_j} v_j \\ & = e^{w} \alpha_{i-1} + e^{k_i} v_i \\[1em] \beta_i & = \sum_{j=1}^i e^{-(i-j)w+k_j} \\ & = e^{w} \beta_{i - 1} + e^{k_i} \\[1em] \text{wkv}_i & = \frac{ e^{u+k_i} v_i + \alpha_{i - 1} }{ e^{u+k_i} + \beta_{i - 1} } \\ \end{aligned}

There are some other components of the model for doing channel mixing, since this "attention" is defined only over time (i.e., the channels do not communicate with each other, which means you can use much less memory bandwidth for doing the computation).

Memory Efficient Attention

Arxiv

Another better attention CUDA kernel. Incorporated into the xFormers package, and into PyTorch 2.0.

out = xformers.ops.memory_efficient_attention(query, key, value)

To explain the basic idea of the paper, consider the attention equation:

$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$

where

$Q$ is the query matrix, with shape $(n, d_k)$
$K$ is the key matrix, with shape $(m, d_k)$
$V$ is the value matrix, with shape $(m, d_v)$
$d_k$ is the key dimension
$\text{Attention}(Q, K, V)$ is the output matrix, with shape $(n, d_v)$

The paper does a decent job of explaining the idea, so I'm going to be extra verbose just to make it very clear what's happening.

The core idea is that, if we're writing custom kernels instead of using vanilla PyTorch, we don't need to instantiate the full intermediate matrices into memory. Instead, we can compute the output value for an index by marching along the rows and columns that are required for that value.

We'll write the above matrices as:

\begin{aligned} Q & = \begin{bmatrix} q_{1, 1} & \cdots & q_{1, n} \\ \vdots & \ddots & \vdots \\ q_{d_k, 1} & \cdots & q_{d_k, n} \end{bmatrix} \\[1em] K & = \begin{bmatrix} k_{1, 1} & \cdots & k_{1, m} \\ \vdots & \ddots & \vdots \\ k_{d_k, 1} & \cdots & k_{d_k, m} \end{bmatrix} \\[1em] V & = \begin{bmatrix} v_{1, 1} & \cdots & v_{1, m} \\ \vdots & \ddots & \vdots \\ v_{d_v, 1} & \cdots & v_{d_v, m} \end{bmatrix} \\ \end{aligned}

We can first consider the values of $QK^T$ :

\begin{aligned} S = QK^T & = \begin{bmatrix} q_{1, 1} k_{1, 1} + \cdots + q_{d_k, 1} k_{d_k, 1} & \cdots & q_{1, 1} k_{1, m} + \cdots + q_{d_k, 1} k_{d_k, m} \\ \vdots & \ddots & \vdots \\ q_{1, n} k_{1, 1} + \cdots + q_{d_k, n} k_{d_k, 1} & \cdots & q_{1, n} k_{1, m} + \cdots + q_{d_k, n} k_{d_k, m} \end{bmatrix} \\ & = \begin{bmatrix} s_{1, 1} & \cdots & s_{1, m} \\ \vdots & \ddots & \vdots \\ s_{n, 1} & \cdots & s_{n, m} \end{bmatrix} \end{aligned}

We then do another matrix multiplication of $e^S$ with $V$ , and then divide by $e^S$ summed over the rows:

e^S V^T = \begin{bmatrix} e^{s_{1, 1}} v_{1, 1} + \cdots + e^{s_{1, m}} v_{1, m} & \cdots & e^{s_{1, 1}} v_{d_v, 1} + \cdots + e^{s_{1, m}} v_{d_v, m} \\ \vdots & \ddots & \vdots \\ e^{s_{n, 1}} v_{1, 1} + \cdots + e^{s_{n, m}} v_{1, m} & \cdots & e^{s_{n, 1}} v_{d_v, 1} + \cdots + e^{s_{n, m}} v_{d_v, m} \end{bmatrix}

We then need to divide by $e^S$ summed over the rows to get our output matrix, but we'll ignore that for now. If we consider a single value of the above matrix:

$(e^S V^T)_{i, j} = e^{s_{i, 1}} v_{j, 1} + \cdots + e^{s_{i, m}} v_{j, m}$

In a vanilla PyTorch implementation, computing this value would require $O(n)$ memory, because we would need to store the intermediate $s$ vector. However, we can compute this value in $O(1)$ memory by processing the summation sequentially. So for each step $k$ in the above summation, we first compute $e^{s_{i, k}}$ , then multiply it by $v_{j, k}$ , and then add it to the running total. We can also keep a running total of the values of $e^{s_{i, k}}$ to get the denominator of the softmax.

Note that there are also tricks we can do here to maintain numerical stability. For example, we can subtract the maximum value of $s_{i, k}$ from each value of $s_{i, k}$ before exponentiating it, for both the numerator and denominator. Alternatively, we can use log-space operations.

Flash Attention

Fast CUDA kernel for attention. Incorporated into the xFormers library, and into PyTorch 2.0. There's a nice glossary of attention implementations in the xFormers package here.

Flash attention seemed to receive a lot more attention (pun intended) than the memory-efficient attention paper, perhaps because of good marketing. But the core idea behind the two papers is the same, and if you look through the implementation for flash attention it is doing exactly what is described above.

The key thing to note is that the major limitation for transformers is memory bandwidth, so we want to cut down on HBM to SRAM copies as much as possible. This is basically what we do with the above reformulation, but the point of calling this method "flash attention" is highlighting that the marching process happens in SRAM without copying anything back to HBM until we have our final value.

Once you understand the above computation, the Triton kernel implementing Flash Attention is actually quite straight-forward to understand.

RoPE

Rotary positional embeddings (RoPE) aren't in themselves a "fast attention" mechanism, but I saw a paper recently which extends them to allow for longer context windows. The idea of the paper is that you can interpolate the RoPE function to get the positional embeddings for intermediate points. Suppose during pre-training you have some context window size $T$ , and you want to increase it by a factor $k$ (to a total context window size $kT$ ). You can fine-tune the model on a small number of examples (around 1000) by multiplying the RoPE function wavelength by $k$ . Interpolating this extended RoPE function is more stable than extrapolating the original RoPE function.

Here's an implementation of rotary embeddings (although there are many references online). It complies with my embeddings API that I use in my projects.

class RotaryEmbeddings(nn.Module):
    def __init__(
        self,
        max_tsz: int,
        embed_dim: int,
        learnable: bool = False,
        base: int = 10_000,
    ) -> None:
        """Defines a rotary embeddings module.

        Args:
            max_tsz: The maximum sequence length.
            embed_dim: The embedding dimension.
            learnable: Whether the embeddings are learnable.
            base: The base for the sinusoidal embeddings.
        """
        super().__init__()

        assert embed_dim % 4 == 0, "Embedding dimension must be divisible by 4."

        self.embed_dim = embed_dim
        self.learnable = learnable
        self.base = base

        cos, sin = self.get_embeddings(max_tsz)
        self.cos, seflf.sin = nn.Parameter(cos, requires_grad=learnable), nn.Parameter(sin, requires_grad=learnable)

    def get_embeddings(self, tsz: int) -> tuple[Tensor, Tensor]:
        half_d = self.embed_dim // 2
        theta = 1.0 / (self.base ** (torch.arange(0, half_d, 2).float() / half_d))
        seq_idx = torch.arange(tsz).float()
        idx_theta = torch.einsum("n,d->nd", seq_idx, theta)
        idx_theta2 = torch.cat([idx_theta, idx_theta], dim=1)
        return idx_theta2.cos(), idx_theta2.sin()

    def _neg_half(self, x: Tensor) -> Tensor:
        quarter_d = self.embed_dim // 4
        return torch.cat([-x[..., quarter_d:], x[..., :quarter_d]], dim=-1)

    def forward(self, x: Tensor, offset: int = 0, times: Tensor | None = None) -> Tensor:
        half_d = self.embed_dim // 2
        x_rope, x_pass = x[..., :half_d], x[..., half_d:]
        neg_half_x = self._neg_half(x_rope)
        cos_part = self.cos[None, offset : offset + x.shape[1]] if times is None else self.cos[times]
        sin_part = self.sin[None, offset : offset + x.shape[1]] if times is None else self.sin[times]
        x_rope = x_rope * cos_part + neg_half_x * sin_part
        return torch.cat((x_rope, x_pass), dim=-1)